van Genuchten Functional Form

This option uses the van Genuchten (1980) retention function.

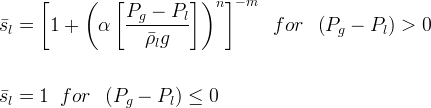
where

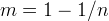
Symbols
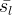	effective aqueous liquid saturation
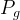	gas pressure, Pa
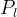	aqueous liquid pressure, Pa
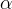	van Genuchten function parameter, 1/m
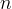	van Genuchten n parameter
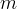	van Genuchten m parameter
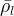	reference aqueous density, kg/m3
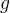	acceleration of gravity, m/s2

Brooks and Corey Functional Form

The Brooks and Corey (1966) retention function is used.

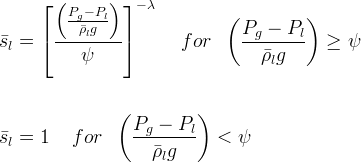
Symbols
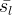	effective aqueous liquid saturation
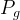	gas pressure, Pa
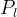	aqueous liquid pressure, Pa
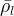	reference aqueous density, kg/m3
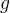	acceleration of gravity, m/s2
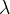	Brooks and Corey lambda parameter
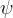	Brooks and Corey function nonwetting fluid entry head, m

Haverkamp Functional Form

The Haverkamp et al. (1977) retention function is used.

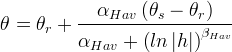
Symbols
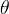	volumetric water content
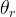	residual water content
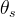	saturated water content
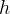	capillary head, m
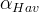	Haverkamp α parameter
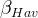	Haverkamp β parameter

Gas Entrapment

This option considers entrapped gas that is immobile and also reduces the pore fraction for the mobile fluid.

A theoretical model for hysteretic saturation functions for aqueous-gas systems was developed by Parker and Lenhard [1987]. A simplified version of this model, analogous to Kaluarachchi and Parker [1992], has been implemented in the STOMP simulator. The model includes effects of gas entrapment during aqueous-phase imbibition paths. Gas entrapment during aqueous-phase imbibition will depend on the aqueous saturation and the current saturation path. The amount of entrapped gas varies linearly between zero and the gas effective residual saturation with the apparent saturation, which varies between the reversal point from main drainage to one. Gas effective residual saturations are computed using an empirical relationship developed by Land [1968] for aqueous-NAPL systems. In this simplified hysteretic model for aqueous-gas systems, gas can be trapped or free, where free gas refers to continuous volumes which advect freely, and trapped gas refers to discontinuous ganglia of gas occluded within the aqueous phase. Occluded gas is assumed to be immobile. The apparent aqueous saturation equals the effective aqueous saturation plus effective trapped gas saturation, as shown in the Equation 1 below. The effective gas saturation equals the effective trapped and free gas saturations, as shown in Equation 3. In hysteretic systems, the residual saturation is independent of capillary pressure.

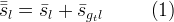
where

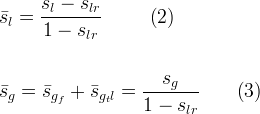
The saturation functions relate gas-aqueous capillary pressure to apparent aqueous saturations, according to equations (4) and (5), for the van Genuchten and Brooks and Corey functions, respectively. The effective trapped gas saturation is computed according to equation (7), which recognizes that entrapped gas cannot exceed the gas present. Land’s parameter for gas-aqueous interfaces is computed according to equation (8).

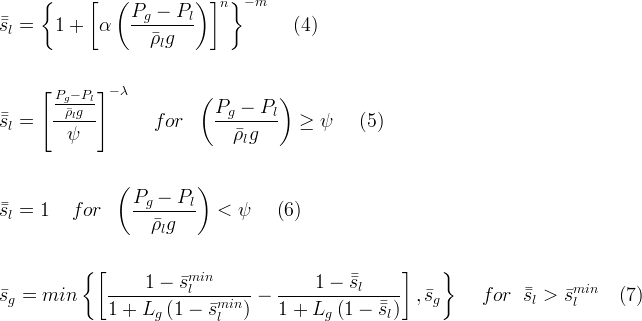
where

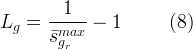
Symbols
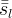	apparent aqueous liquid saturation
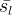	effective aqueous liquid saturation
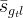	effective gas saturation trapped by aqueous phase
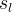	actual aqueous liquid saturation
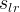	actual aqueous liquid residual saturation
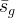	effective gas saturation
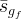	effective free gas saturation
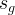	actual gas saturation
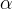	van Genuchten function parameter, 1/m
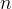	van Genuchten n parameter
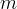	van Genuchten m parameter
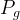	gas pressure, Pa
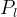	aqueous liquid pressure, Pa
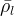	reference aqueous density, kg/m3
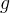	acceleration of gravity, m/s2
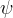	Brooks and Corey function nonwetting fluid entry head, m
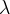	Brooks and Corey parameter
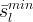	minimum effective aqueous liquid saturation
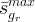	maximum effective residual gas saturation
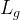	Land's parameter for gas-aqueous interface

Webb Extension

To extend the saturation function below the aqueous residual saturation, functional extensions are required. STOMP-CO2 and -CO2E recognize the Webb (2000) model. This function works with both the van Genuchten and Brooks and Corey characteristics functions, without requiring additional input as the oven-dried head is assumed to be equal to a capillary pressure of 109 Pa (~105 m).

Fractured Media (Equivalent Continuum)

This option is used for a fractured medium. The retention properties for both the fracture and the matrix are needed. Dual porosity functions or equivalent continuum models for aqueous-gas systems relate the gas-aqueous capillary pressure to the bulk aqueous saturation for fractured geologic media through two functions [Klavetter and Peters 1986; Nitao 1988]. One function relates the gas aqueous capillary pressure to the matrix aqueous saturation and the other relates the gas-aqueous capillary pressure to the fracture aqueous saturation. The pivotal assumption associated with the dual porosity function is that the fracture and matrix pressures are in equilibrium. This assumption neglects transient fracture-matrix interactions. Fracture and matrix effective saturations can be computed with either van Genuchten or Brooks and Corey functions above. The bulk aqueous saturation is computed by combining the fracture and matrix aqueous saturations and diffusive porosities:

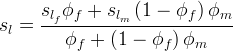
where the actual saturations are computed from effective saturations, according to

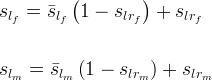
Symbols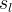
	actual aqueous liquid saturation
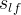	actual aqueous liquid saturation of the fracture material
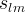	actual aqueous liquid saturation of the matrix material
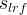	actual aqueous liquid residual saturation of the fracture material
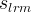	actual aqueous liquid residual saturation of the matrix material
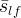	effective aqueous liquid saturation of the fracture material
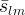	effective aqueous liquid saturation of the matrix material
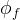	diffusive porosity of the fracture material
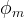	diffusive porosity of the matrix material

Tabular Input

This option accepts tabulated retention data. The default is the data of pressure head and saturation data pairs and linear interpolation is used between data points. Alternately, water content vs capillary head can be provided using the keyword "water content." Other interpolation schemes that can be specified are linear-log, cubic spline, or cubic-spline-log.