STOMP User Guide

Subsurface Transport Over Multiple Phases

Numerical Solutions

STOMP uses Newton-Raphson linearization to solve the set of nonlinear algebraic equations formed by the discretized governing equations. This scheme has two major computational components: (1) to compute the Jacobian matrix and solution vector elements and (2) to solve the resulting linear system of equations.

Newton-Raphson Iteration
Linear System Solvers

The nonlinearities in the coupled flow and energy transport system of equations are resolved through the application of the iterative Newton-Raphson technique. The Newton-Raphson linearization technique is an iterative method for solving nonlinear algebraic equations of the form

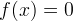
where f(x) is differentiable in x. The linearization concept approximates f(x) with suitable tangents.

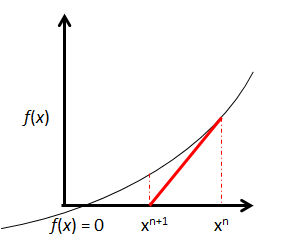
NR Iteration (Conceptual Plot)

Each iteration yields a new estimate of x as the intersection of the tangent to the function f(x) at the previous estimate of x and the abscissa axis, according to

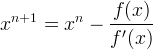
In this formulation f(x) is considered the equation residual. For convergent systems, the residual decreases quadratically with iteration. In multiple variable systems, as with the coupled flow and energy transport system, the scalar function, f(x), is replaced with a vector function R(x), according to

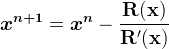
The vector function, R(x), represents the system of nonlinear algebraic equations produced from discretizing the conservation equations for component mass and energy. The vector of unknowns, x, represents the set of primary variables for the system, which are determined by the operational mode and phase conditions. This can be rewritten in terms of increments to the primary variables, according to

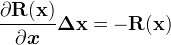
The partial derivatives shown above form the Jacobian matrix.

Jacobian example for a 1D system

For simplification, a one-dimensional system involving the solution of the water mass, air mass, and energy conservation equations will be considered. The system of linear equations that result from applying the Newton-Raphson linearization technique to this system of nonlinear algebraic equations for a computational domain with “n” nodes is shown below.

Here, each Jacobian matrix element represents a block matrix of order three, according to

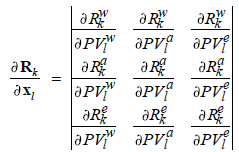
Each unknown vector element represents a vector of increments to the primary variables of order three, according to

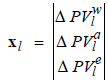
Each solution vector element represents a vector of equation residuals of order three, according to

Info

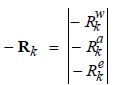
For a two-dimensional system involving the solution of the water mass, air mass, and energy conservation equations, the Jacobian matrix would contain two extra bands of block matrices: one below and one above the diagonal band. These extra bands would be located one half-band width from the main diagonal band, where the half-band width equaled the lesser of the number of nodes per row or column for a two-dimensional grid.

A three-dimensional grid would contain four extra bands of block matrices, two below and two above the diagonal band. The furthest bands would be located one half-band width from the main diagonal band, where the halfband width equaled the least number of nodes in a plane. For example, a three-dimensional Cartesian grid with 20 nodes in the “X” coordinate direction, 30 nodes in the “Y” coordinate direction, and 40 nodes in the “Z” coordinate direction, would have a half-band width of 600.

The linear system of equations produced during Newton-Raphson iteration is solved with either a direct or iterative linear system solver. The user must choose one of two solver options when requesting the source code. The banded matrix solution algorithm from LINPACK (bd) solver is a direct solver included with the source code and is appropriate for problems with less than 10,000 unknowns. For larger problems, the user should request the linear system solver (lis).

Banded matrix (bd solver)

The banded matrix solution algorithm was extracted from the LINPACK subroutines (Dongarra et al. 1979) for general nonsymmetric band matrices. The algorithm operates on band matrices by decomposing the matrix into an upper triangular and lower triangular matrix. The matrix product of the lower triangular matrix with the upper triangular matrix equals the original band matrix (i.e., A = L U, where A is the band matrix, L is the lower triangular matrix and U is the upper triangular matrix). The system of linear equations, A x = b, is solved with the above decomposition or factorization by solving successively L (U x) = b. This factorization procedure produces nonzero elements outside the bands of the original band matrix. If m_l equals the half-band width of the Jacobian coefficient matrix (the Arid-ID engineering simulator produces band matrices with equal lower and upper band widths), then the two triangular factors have band widths of m_l and 2m_l. Storage must be provided for the extra m_l diagonals. This is illustrated for a one-dimensional problem of five nodes and two-solved mass conservation equations. The Jacobian coefficient matrix for this problem would appear as shown.

Jacobian Coefficient Matrix

The band storage requires 3 m_l + 1 = 10 rows of storage arranged as shown.

Storage Matrix

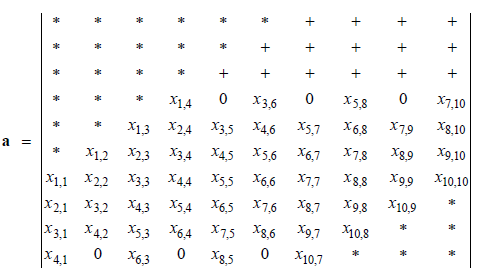
The * indicates elements which are never referenced but storage space must be provided. The + indicates elements which may be occupied during the factorization process. The original Jacobian coefficient matrix is referred to as A and its storage counterpart as a; then the columns of A are stored in the columns of a, and the diagonals of A are stored in the rows of a, such that the principal diagonal is stored in row 2 m_l + 1 of a.

Reference:

Dongarra, JJ., J Bunch, C Moler and GW Stewart. 1979. LINPACK User’s Guide. SIAM, Philadelphia, PA.

Linear system solver (lis)

Lis (Library of Iterative Solvers for linear systems) is a parallel software library for solving discretized linear equations and eigenvalue problems that arise in the numerical solution of partial differential equations using iterative methods.