STOMP User Guide
STOMP User Guide
Gas Relative Permeability Card Options
The gas relative permeability functions relate phase saturations with gas relative permeability. The Gas Relative Permeability Card is used to specify model options and parameters. Every rock/soil type defined on the Rock/Soil Zonation Card must be referenced. With the IJK Indexing option, node dependent parameters are entered via external files and node independent parameters are entered directly on the card. The Mualem and Burdine gas relative permeability functions are also dependent on the saturation function type and are strictly applicable to the van Genuchten (1980) and Brooks and Corey (1966) functions. For these functions, either the van Genuchten 'm' parameter or the Brooks and Corey 'λ' parameter can be defaulted to the values entered or defaulted with the saturation function. Functional forms for the gas relative permeability-saturation functions are preferred, but tabular input is acceptable. By default, tabular data will be interpolated using linear interpolation, whereas values beyond the table limits will be assigned either the table minimum or maximum values appropriately.
Effective Saturations
Mobile saturations are scaled by the residual aqueous liquid saturation to determine effective saturations for use with common relative permeability models.
The effective aqueous liquid saturation:
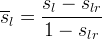
The effective aqueous nonaqueous liquid saturation:
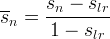
The effective gas saturation:
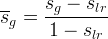
The wetting phases are combined for a total effective liquid saturation:
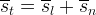
| Symbols | |
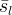 |
effective aqueous liquid saturation |
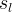 |
actual aqueous liquid saturation |
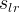 |
actual aqueous liquid residual saturation |
Burdine
The Burdine (1953) relative permeability function is described as
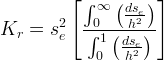
Gas phase relative permeability can be computed as a function of Gas saturation from knowledge of the soil-moisture retention function and the pore distribution model of Burdine [1953]. If the van Genuchten and Brooks and Corey soil-moisture retention functions are used, closed-form expressions for fluid phase relative permeability can be derived. Using the van Genuchten soil-moisture retention function, the Gas phase relative permeability appears as shown:
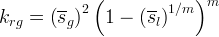
Using the Brooks and Corey soil-moisture retention function, the Gas phase relative permeability appears as shown:
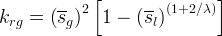
Mualem
The Mualem(1976) relative permeability function is described as
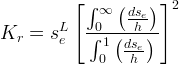
where L = 0.5.
Gas phase relative permeability can be computed as a function of Gas saturation from knowledge of the soil-moisture retention function and the pore distribution model of Mualem [1976]. If the van Genuchten and Brooks and Corey soil-moisture retention functions are used, closed-form expressions for fluid phase relative permeability can be derived. Using the van Genuchten soil-moisture retention function, the Gas relative permeability appears as shown:
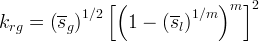
Using the Brooks and Corey soil-moisture retention function, the Gas phase relative permeability appears as shown:
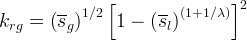
Modified Mualem
Irreducible Mualem
Mulaem with Polman
The Mualem (1976) relative permeability model is used to calculate the vertical permeability and the Polmann (1990) model is used to calculate horizontal permeability.
Polmann (1990) used a stochastic model to evaluate tension-dependent anisotropy. The Gardner (1958) relationship was used to describe unsaturated hydraulic conductivity as a function of saturated hydraulic conductivity and tension. Using a linear correlation model between the zero-tension intercept and β, Polmann (1990) presented a generalized model that accounts for the cross-correlation of the local soil property (i.e., lnKs and β) residual fluctuations. Compared against the uncorrelated lnKs and β model, the partial correlation of the properties was shown to have a significant impact on the magnitude of the effective parameters derived from the stochastic theory. The Polmann (1990) equations for deriving the effective parameters for strongly stratified porous media are as shown below.
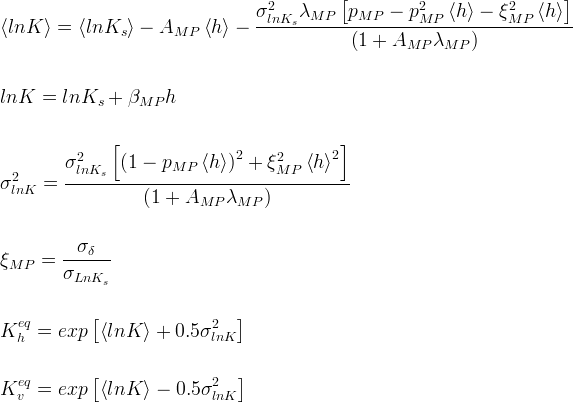
A modified version of the original Polmann model is implemented in STOMP. This version uses a single segment of the log-linear K(h) function. Because the Polmann model is based on the log-linear hydraulic function, it may be applicable only to a relatively narrow pressure head range over which the parameters are derived. Extrapolating the derived hydraulic function to other pressure head conditions may cause significant error or even physically incorrect results (e.g., the predicted hydraulic conductivity in the horizontal direction may increase with decreasing saturation, which is physically incorrect). It calculates an anisotropy coefficient (Can) and the hydraulic conductivity in the horizontal direction (Kh). The modified model also requires user specified maximum (Canmax) and minimum (Canmin) limits of the anisotropy coefficient. If computed values of Can are outside these limits, the values are truncated as shown in the equations below:
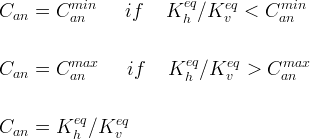
| Symbols | |
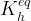 |
equivalent unsaturated hydraulic conductivity in the horizontal direction, m/s |
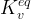 |
equivalent unsaturated hydraulic conductivity in the vertical direction, m/s |
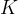 |
unsaturated hydraulic conductivity (pressure dependent), m/s |
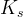 |
saturated hydraulic conductivity, m/s |
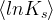 |
mean of LnKs |
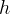 |
capillary head, m |
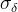 |
standard deviation of the residuals in the LnKs vs. β regression for all the samples considered |
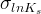 |
standard deviation of LnKs |
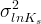 |
variance of LnKs |
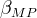 |
slope between LnKs and h |
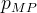 |
slope of LnKs vs. β regression line for the samples considered |
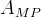 |
mean slope of β for LnK vs. h regression |
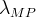 |
vertical correlation length for LnKs |
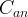 |
anisotropy coefficient |
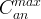 |
maximum value of anisotropy coefficient |
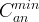 |
minimum value of anisotropy coefficient |
Brooks, RH and AT Corey. 1966. "Hydraulic Properties of Porous Media Affecting Fluid Flow," Proc. ASCE J. Irrig. Drain. Div. , 92:61-68.
Mualem, Y. 1976. "A New Model for Predicting the Hydraulic Conductivity of Unsaturated Porous Media," Water Resources Research, 12:513-522.
van Genuchten, MT. 1980. "A Closed-Form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils," Soil Science Society of America Journal, 44:892-898.
Fatt and Klikoff
Aqueous- and gas-phase relative permeability are computed according to the Fatt and Klikoff [1959] models from the conventionally defined effective Gas saturation according to equations (1) and (2), respectively.
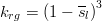
Corey Model
Aqueous- and gas-phase relative permeability can be computed from modified expressions for effective Gas saturation according to the empirical model of Corey [1977]. The model of Corey accounts for trapped air through a modification to the definition of the effective Gas saturation according to equation (1). The Corey functions for aqueous- and gas-phase relative permeability are computed according to equations (2) and (3), respectively.
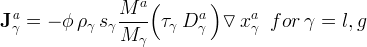
Free Corey
The free Corey is a modified version of the empirical model of Corey [1977]. The model accounts for trapped air through a modification to the definition of the effective Gas saturation according to equation (1). The free Corey function for Gas-phase relative permeability is computed according to equation (2).
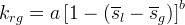
| Symbols | ||
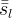 |
apparent Gas liquid saturation | |
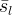 |
effective Gas liquid saturation | |
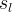 |
actual Gas liquid saturation | |
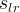 |
actual Gas liquid residual saturation | |
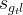 |
actual gas saturation trapped by Gas phase | |
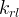 |
Gas relative permeability | |
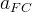 |
Free Corey model parameter | |
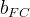 |
Free Corey model parameter | |
Constant
The relative permeability is constant regardless of saturation.
Tabular
This option accepts tabulated relative permeability data. The default is the data of Gas saturation and Gas relative permeability data pairs and linear interpolation is used between data points; a cubic spline interpolation scheme can also be specified. Alternately, capillary head vs relative permeability can be provided using the keyword "head." Other interpolation schemes that can be specified for capillary head vs. Gas relative permeability are log capillary head vs relative permeability, cubic spline, or cubic spline for log capillary head vs relative permeability.
Fractured Media
Dual porosity functions or equivalent continuum models [Klavetter and Peters 1986; Nitao 1988] relate bulk fluid phase relative permeabilities to those for the fracture and matrix according to equations (1) and (2). Dual porosity models require the assumption that fracture and matrix fluid pressures are in equilibrium, which inherently neglects transient fracture-matrix interactions. Fracture and matrix relative permeabilities are computed from either the Burdine or Mualem models using either the van Genuchten or Brooks and Corey soil moisture retention functions. In these functions the effective aqueous and gas saturations are replaced with the corresponding values for the fracture and matrix components of the soil. For example, the fracture and matrix Gas relative permeabilities for the Burdine model with the Brooks and Corey soil-moisture retention function are shown in equations (3) and (4), respectively.
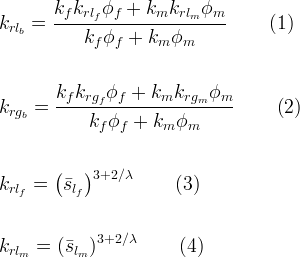
| Symbols | |
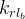 |
bulk Gas relative permeability |
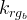 |
bulk gas relative permeability |
 |
intrinsic permeability of the fracture material, m2 |
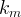 |
intrinsic permeability of the matrix material, m2 |
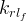 |
Gas relative permeability of the fracture material |
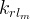 |
Gas relative permeability of the matrix material |
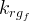 |
gas relative permeability of the fracture material |
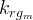 |
gas relative permeability of the matrix material |
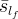 |
effective Gas liquid saturation of the fracture material |
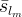 |
effective Gas liquid saturation of the matrix material |
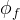 |
diffusive porosity of the fracture material |
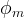 |
diffusive porosity of the matrix material |
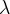 |
Brooks and Corey parameter |
Burdine, NT. 1953. "Relative Permeability Calculation from Size Distribution Data," Trans. AIME, 198:71-78.
Corey, AT. 1977. Mechanics of Heterogeneous Fluids in Porous Media, Fort Collins, Colorado.
Fatt , I and WA Klikoff Jr. 1959. "Effect of Fractional Wettability on Multiphase Flow through Porous Media," AIME Trans, 215:426-429.
Gardner, WR. 1958. "Some Steady-State Solutions of the Unsaturated Moisture Flow Equation with Applications to Evaporation from a Water Table," Soil Science, 85:228-232.
Haverkamp, R, M Vauclin, J Touma, PJ Wierenga, and G Vachaud. 1977. "A Comparison of Numerical Simulation Models for One-Dimensional Infiltration," Soil Sci. Soc. Am. J., 41:285-294.
Klavetter, E.A., Peters, R.R., 1986. Estimation of hydrologic properties of unsaturated fractured rock mass. Sandia National Laboratories, Albuquerque, NM.
Mualem, Y. 1976. "A New Model for Predicting the Hydraulic Conductivity of Unsaturated Porous Media," Water Resources Research, 12:513-522.
Nitao, J.J., 1988. Numerical modeling of the thermal and hydrological environment around a nuclear waste package using the equivalent continuum approximation: horizontal emplacement. Lawrence Livermore National Laboratory, Livermore, CA.
Polmann, DJ. 1990. "Application of Stochastic Methods to Transient Flow and Transport in Heterogeneous Unsaturated Soils," PhD, Massachusetts Institute of Technology, Cambridge, MA.
Touma, J. & Vauclin, M. 1986. Experimental and numerical analysis of two-phase infiltration in a partially saturated soil. Trans. Porous Media, 1, 27-55